235. Точки A
и B
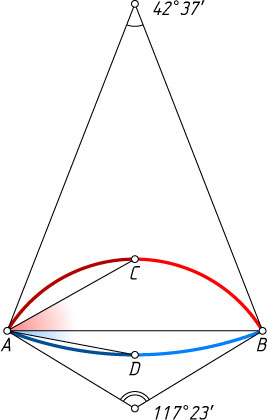
соединены двумя дугами окружностей, обращёнными выпуклостями в разные стороны: \smile ACB=117^{\circ}23'
и \smile ADB=42^{\circ}37'
. Середины C
и D
этих дуг соединены с точкой A
. Найдите угол CAD
.
Ответ. 40^{\circ}
.
Указание. Луч AB
проходит между сторонами угла CAD
. Поэтому \angle CAD=\angle CAB+\angle BAD
.
Решение. Поскольку луч AB
проходит между сторонами угла CAD
, то
\angle CAD=\angle CAB+\angle BAD=\frac{1}{2}\smile BC+\frac{1}{2}\smile BD=
=\frac{\frac{1}{2}\smile ACB+\frac{1}{2}\smile ADB}{2}=\frac{\smile ACB+\smile ADB}{4}=40^{\circ}.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 22, с. 36
