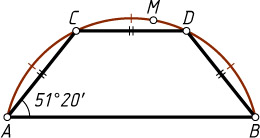
237. В круговой сегмент AMB
вписана трапеция ACDB
, у которой AC=CD
и \angle CAB=51^{\circ}20'
. Найдите угловую величину дуги AMB
.
Ответ. 154^{\circ}
.
Указание. Трапеция, вписанная в окружность, — равнобедренная. Если равны хорды, то равны и соответствующие им дуги.
Решение. Эта трапеция — равнобедренная. Кроме того, \cup BDC=2\angle CAB
. Поскольку D
— середина дуги BDC
, то каждая из трёх дуг, на которые точки C
и D
делят дугу AMB
, равны. Поэтому угловая величина каждой из них равна 51^{\circ}20'
. Следовательно,
\cup AMB=3\cdot51^{\circ}20'=154^{\circ}.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 2, с. 36
