239. Угол при вершине равнобедренного треугольника равен 40^{\circ}
. Одна из боковых сторон служит диаметром полуокружности, которая делится другими сторонами на три части. Найдите эти части.
Ответ. 40^{\circ}
, 40^{\circ}
, 100^{\circ}
.
Указание. Точка пересечения окружности с основанием треугольника — основание высоты, проведённой из его вершины.
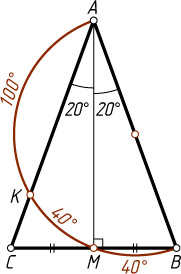
Решение. Пусть AB
— диаметр окружности, M
— точка её пересечения с основанием BC
, K
— точка пересечения с боковой стороной AC
. Тогда AM
— высота, а значит, биссектриса равнобедренного треугольника BAC
. Следовательно,
\cup BM=\cup MK=40^{\circ},~\cup KA=180^{\circ}-2\cdot40^{\circ}=100^{\circ}.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 26, с. 36
