241. Постройте прямоугольный треугольник по гипотенузе и высоте, опущенной из вершины прямого угла на гипотенузу.
Указание. Постройте геометрическое место точек, из которого данный отрезок (гипотенуза) виден под прямым углом.
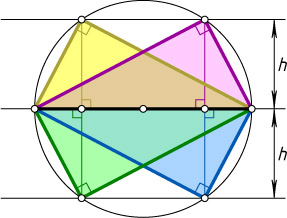
Решение. Построим на данной гипотенузе как на диаметре окружность и найдём точки пересечения этой окружности с прямыми, параллельными прямой, содержащей гипотенузу, и отстоящими от неё на расстояние, равное данной высоте. Полученные точки (если они есть) — вершины прямых углов искомых треугольников.

Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 29, с. 36