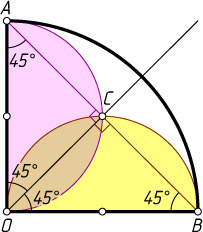
245. На сторонах OA
и OB
четверти AOB
круга построены как на диаметрах полуокружности ACO
и OCB
, пересекающиеся в точке C
. Докажите, что:
1) прямая OC
делит угол AOB
пополам;
2) точки A
, C
и B
лежат на одной прямой;
3) дуги AC
, CO
и CB
равны между собой.
Указание. Соответствующие дуги равных полуокружностей, стягиваемых равными хордами, равны между собой. Если OC\perp AC
и OC\perp BC
, то точки A
, B
и C
лежат на одной прямой.
Решение. Дуги OC
двух полуокружностей равны, так как они стягиваются равными хордами. Поэтому равны и дополняющие их до равных полуокружностей дуги AC
и BC
. Следовательно, равны опирающиеся на них вписанные углы AOC
и BOC
.
\angle ACO=\angle BCO=90^{\circ}
как вписанные углы, опирающиеся на диаметры. Поэтому ACB
— одна прямая.
\cup AC=\cup CO=\cup CB
, так как опирающиеся на эти дуги вписанные углы равны по 45^{\circ}
.
Источник: Гальперин Г. А., Толпыго А. К. Московские математические олимпиады. — М.: Просвещение, 1988. — № 33, с. 37
