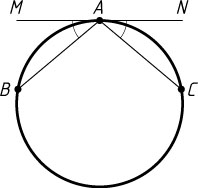
247. AB
и AC
— равные хорды, MAN
— касательная, угловая величина дуги BC
, не содержащей точки A
, равна 200^{\circ}
. Найдите углы MAB
и NAC
.
Ответ. \angle MAB=\angle NAC=40^{\circ}
или \angle MAB=\angle NAC=140^{\circ}
.
Указание. Рассмотрите все возможные расположения точек M
, A
, C
, и примените теорему об угле между касательной и хордой.
Решение. Заметим, что
\cup CAB=360^{\circ}-200^{\circ}=160^{\circ},~\cup AB=\cup AC=\frac{160^{\circ}}{2}=80^{\circ}.
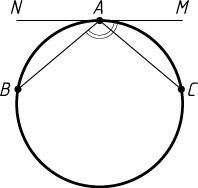
Если угол MAB
— острый, то
\angle MAB=\frac{\cup AB}{2}=40^{\circ}.
Тогда и \angle NAC=40^{\circ}
.
Если же угол MAB
— тупой, то
\angle MAB=180^{\circ}-40^{\circ}=140^{\circ}.
Тогда и \angle NAC=140^{\circ}
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 35, с. 37
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.2, с. 103

