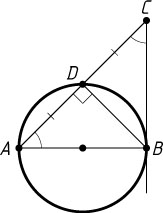
249. В окружности проведён диаметр AB
. Прямая, проходящая через точку A
, пересекает в точке C
касательную к окружности, проведённую через точку B
. Отрезок AC
делится окружностью пополам. Найдите угол BAC
.
Ответ. 45^{\circ}
.
Указание. Вписанный угол, опирающийся на диаметр, равен 90^{\circ}
.
Решение. Пусть окружность пересекает отрезок AC
в точке D
. В прямоугольном треугольнике ABC
высота BD
является медианой, значит, этот треугольник — равнобедренный. Следовательно, \angle BAC=\angle BAD=45^{\circ}
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 37, с. 37
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.1, с. 60
