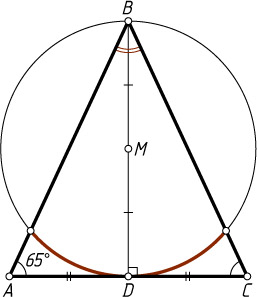
250. M
— середина высоты BD
в равнобедренном треугольнике ABC
. Точка M
служит центром окружности радиуса MD
. Найдите угловую величину дуги окружности, заключённой между сторонами BA
и BC
, если \angle BAC=65^{\circ}
.
Ответ. 100^{\circ}
.
Указание. Угловая величина дуги в два раза больше угловой величины соответствующего вписанного угла.
Решение. Искомая величина дуги в два раза больше угловой величины вписанного угла ABC
, т. е. равна
2(180^{\circ}-2\cdot65^{\circ})=100^{\circ}.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 38, с. 37
