251. Окружность разделена точками A
, B
, C
, D
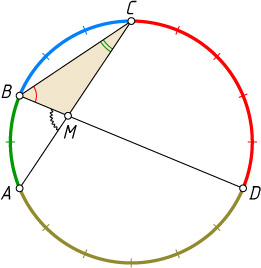
так, что \cup AB:\cup BC:\cup CD:\cup DA=2:3:5:6
. Проведены хорды AC
и BD
, пересекающиеся в точке M
. Найдите угол AMB
.
Ответ. 78^{\circ}45'
.
Указание. AMB
— внешний угол треугольника MBC
.
Решение. По теореме о внешнем угле треугольника
\angle AMB=\angle DBC+\angle ACB=\frac{1}{2}\cup DC+\frac{1}{2}\cup AB=
=\frac{7}{2+3+5+6}\cdot\frac{1}{2}\cdot360^{\circ}=78^{\circ}45'.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 39, с. 37
