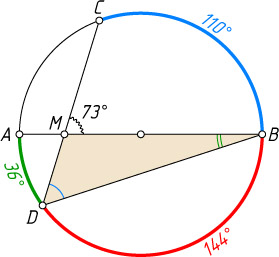
252. Диаметр AB
и хорда CD
пересекаются в точке M
, \angle CMB=73^{\circ}
, угловая величина дуги BC
равна 110^{\circ}
. Найдите величину дуги BD
.
Ответ. 144^{\circ}
.
Указание. CMB
— внешний угол треугольника MDB
.
Решение. Поскольку CMB
— внешний угол треугольника MDB
, то
\angle ABD=\angle CMB-\angle CDB=73^{\circ}-55^{\circ}=18^{\circ}.
Следовательно,
\cup AD=36^{\circ},~\cup BD=180^{\circ}-36^{\circ}=144^{\circ}.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 40, с. 37
