255. Три равные окружности радиуса R
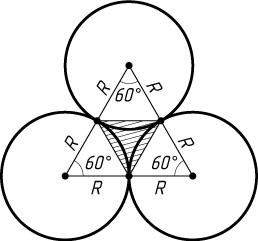
касаются друг друга внешним образом. Найдите стороны и углы треугольника, вершинами которого служат точки касания.
Ответ. R
, 60^{\circ}
, 60^{\circ}
, 60^{\circ}
.
Указание. Рассмотрите равносторонний треугольник с вершинами в центрах окружностей.
Решение. Рассмотрим треугольник с вершинами в центрах окружностей. Поскольку линия центров двух касающихся окружностей проходит через точку касания, его стороны равны 2R
. Стороны искомого треугольника являются его средними линиями, поэтому равны R
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 49(1), с. 33
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.1, с. 67
