256. С помощью циркуля и линейки впишите в данную окружность три равных окружности, которые касались бы попарно между собой и данной окружности.
Указание. Опишите вокруг окружности равносторонний треугольник. В треугольники с вершинами в центре данной окружности и в вершинах построенного треугольника впишите окружности.
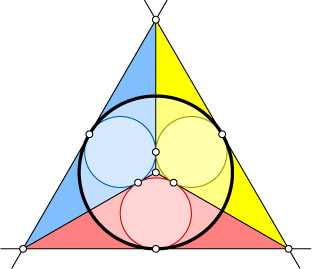
Решение. Разделим данную окружность на три равные части. Через точки деления проведём касательные к окружности. Вершины треугольника, образованного касательными, соединим с центром окружности. Получим три тупоугольных треугольника, в каждый из которых впишем окружность.
Из равенства этих треугольников следует равенство их вписанных окружностей. Из равенства касательных, проведённых к окружности из одной точки, следует, что эти окружности касаются между собой.

Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 49(2), с. 33
Источник: Пойа Д. Математическое открытие. — М.: Наука, 1970. — № 16, с. 39