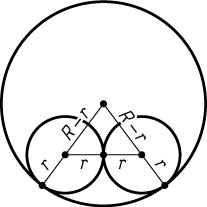
257. Две равные окружности касаются изнутри третьей и касаются между собой. Соединив три центра, получим треугольник с периметром 18. Найдите радиус большей окружности.
Ответ. 9.
Указание. Линия центров двух касающихся окружностей проходит через их точку касания.
Решение. Пусть радиусы данных окружностей равны r
, r
и R
(r\lt R)
. Линия центров двух касающихся окружностей проходит через точку касания, значит, стороны указанного треугольника равны R-r
, R-r
и 2r
. Поэтому
R-r+R-r+2r=2R=18.
Следовательно, R=9
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 50, с. 33
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.2, с. 67
