261. С помощью циркуля и линейки постройте окружность, которая проходила бы через данную точку и касалась бы данной окружности в данной на ней точке.
Указание. Центр искомой окружности принадлежит пересечению двух геометрических мест точек.
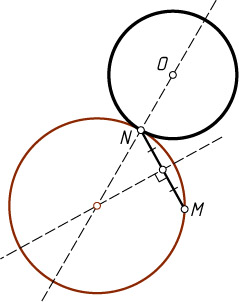
Решение. Пусть M
— данная точка, N
— точка на данной окружности с центром O
. Рассмотрим случай, когда точки M
и N
различны и точка M
не лежит на касательной к данной окружности, проведённой в точке N
.
Поскольку искомая окружность касается данной в точке N
, то её центр расположен на прямой ON
. Поскольку искомая окружность проходит через точки M
и N
, то её центр лежит на серединном перпендикуляре к отрезку MN
. В этом случае задача имеет единственное решение.
Остальные случаи очевидны.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 53(2), с. 34
