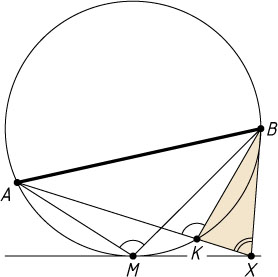
264. Дана окружность с хордой и касательной, причём точка касания лежит на меньшей из двух дуг, стягиваемых хордой. Найдите на касательной точку, из которой хорда видна под наибольшим углом.
Ответ. Точка касания.
Указание. Докажите, что искомая точка — точка касания. Используйте свойство внешнего угла треугольника.
Решение. Пусть M
— точка касания, AB
— хорда, X
— произвольная точка касательной, отличная от M
. Предположим, что отрезок AX
пересекает дугу AMB
в точке K
. Тогда AKB
— внешний угол треугольника KXB
. Поэтому \angle AMB=\angle AKB\gt\angle AXB
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 45, с. 38
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 11.23, с. 275
