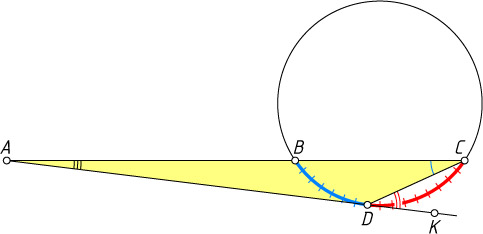
265. Секущая ABC
отсекает дугу BC
, содержащую 112^{\circ}
; касательная AD
точкой касания D
делит эту дугу в отношении 7:9
. Найдите \angle BAD
.
Ответ. 7^{\circ}
.
Указание. Рассмотрите внешний угол треугольника ADC
, смежный с углом ADC
.
Решение. Пусть K
— точка, лежащая на продолжении касательной AD
за точку D
. Угол KDC
— внешний для треугольника DAC
. Поэтому
\angle A=\angle KDC-\angle DCB=\frac{1}{2}\cup CD-\frac{1}{2}\cup DB=
=\frac{1}{2}\left(\frac{9}{16}\cdot112^{\circ}-\frac{7}{16}\cdot112^{\circ}\right)=7^{\circ}.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 46, с. 38
