266. Из концов дуги в 200^{\circ}
проведены касательные до взаимного пересечения. Найдите угол между ними.
Ответ. 20^{\circ}
.
Указание. Проведите радиусы в точки касания.
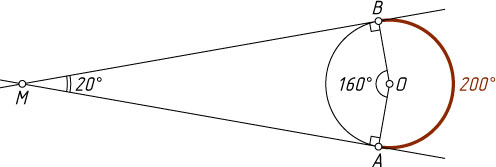
Решение. Пусть A
и B
— точки касания, O
— центр данной окружности, M
— точка пересечения касательных. Тогда
\angle AOB=360^{\circ}-200^{\circ}=160^{\circ}.
Поскольку OA\perp AM
и OB\perp BM
, то
\angle AMB=180^{\circ}-\angle AOB=180^{\circ}-160^{\circ}=20^{\circ}.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 47, с. 38
