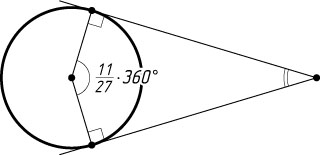
268. Хорда делит окружность в отношении 11:16
. Найдите угол между касательными, проведёнными из концов этой хорды.
Ответ. 33^{\circ}20'
.
Указание. Найдите угловую величину соответствующего центрального угла.
Решение. Угловая величина меньшей из двух дуг равна
\frac{11}{27}\cdot360^{\circ}=\frac{11}{3}\cdot40^{\circ}.
Следовательно, угол между касательными равен
180^{\circ}-\frac{11}{3}\cdot40^{\circ}=33^{\circ}20'.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 48, с. 38
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.19, с. 104
