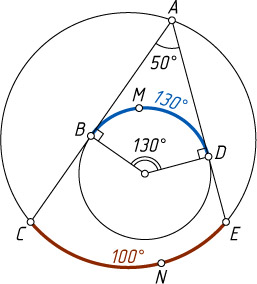
269. Внутри данной окружности находится другая окружность; ABC
и ADE
— хорды большей окружности, касающиеся меньшей окружности в точках B
и D
; BMD
— меньшая из двух дуг между точками касания; CNE
— дуга между концами хорд. Найдите угловую величину дуги CNE
, если дуга BMD
содержит 130^{\circ}
.
Ответ. 100^{\circ}
.
Указание. Угол между касательными, проведёнными из точки A
к меньшей окружности, и соответствующий центральный угол меньшей окружности дополняют друг друга до 180^{\circ}
.
Решение. Угол между касательными, проведёнными из точки A
к меньшей окружности, и соответствующий центральный угол меньшей окружности дополняют друг друга до 180^{\circ}
. Следовательно,
\angle CAE=180^{\circ}-130^{\circ}=50^{\circ},~\cup CNE=2\angle CAE=100^{\circ}.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 50, с. 38
