271. Окружность разделена в отношении 5:9:10
и через точки деления проведены касательные. Найдите наибольший угол в полученном треугольнике.
Ответ. 105^{\circ}
.
Указание. Угол между касательными, проведёнными из одной точки к окружности, дополняет соответствующий центральный угол до 180^{\circ}
.
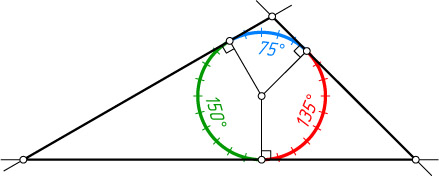
Решение. Найдём получившиеся дуги:
\frac{5}{24}\cdot360^{\circ}=75^{\circ},~\frac{9}{24}\cdot360^{\circ}=135^{\circ},~\frac{10}{24}\cdot360^{\circ}=150^{\circ}.
Углы треугольника дополняют их до 180^{\circ}
. Наибольший угол треугольника равен 180^{\circ}-75^{\circ}=105^{\circ}
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 52, с. 39
