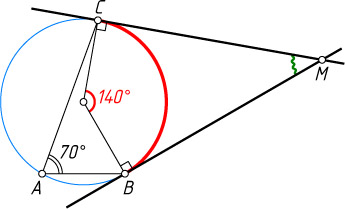
272. AB
и AC
— две хорды, образующие угол BAC
, равный 70^{\circ}
. Через точки B
и C
проведены касательные до пересечения в точке M
. Найдите \angle BMC
.
Ответ. 40^{\circ}
.
Указание. Угол между касательными, проведёнными из одной точки к окружности, дополняет соответствующий центральный угол до 180^{\circ}
.
Решение. \smile BC=2\angle BAC=140^{\circ}
, \angle BMC=180^{\circ}-2\angle BAC=180^{\circ}-140^{\circ}=40^{\circ}
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 53, с. 39.
