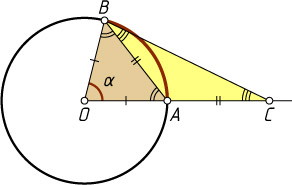
274. Угловая величина дуги AB
равна \alpha\lt180^{\circ}
. На продолжении радиуса OA
отложен отрезок AC
, равный хорде AB
, и точка C
соединена с B
. Найдите угол ACB
.
Ответ. 45^{\circ}-\frac{\alpha}{4}
.
Указание. Примените теорему о внешнем угле треугольника.
Решение. BAO
— внешний угол равнобедренного треугольника CAB
, угол BAO
равен 90^{\circ}-\frac{\alpha}{2}
, а угол ACB
равен половине угла BAO
. Поэтому
\angle ACB=45^{\circ}-\frac{\alpha}{4}.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 55, с. 39
