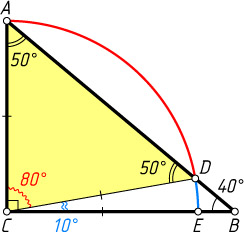
275. В треугольнике ABC
угол C
— прямой. Из центра C
радиусом AC
описана дуга ADE
, пересекающая гипотенузу в точке D
, а катет CB
— в точке E
. Найдите угловые величины дуг AD
и DE
, если \angle B=40^{\circ}
.
Ответ. 80^{\circ}
, 10^{\circ}
.
Указание. Треугольник ACD
— равнобедренный.
Решение. \angle A=90^{\circ}-\angle B=50^{\circ},
треугольник ACD
— равнобедренный,
\angle ACD=180^{\circ}-2\angle A=80^{\circ},~\angle DCB=90^{\circ}-\angle ACD=10^{\circ}.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 56, с. 39
