282. Боковая сторона равнобедренного треугольника равна 2, угол при вершине равен 120^{\circ}
. Найдите диаметр описанной окружности.
Ответ. 4.
Указание. Боковая сторона данного треугольника видна из центра описанной окружности под углом 60^{\circ}
.
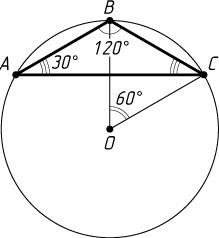
Решение. Боковая сторона BC
равнобедренного треугольника ABC
видна из центра O
описанной окружности под углом 60^{\circ}
, так как на дугу BC
опирается вписанный угол CAB
, равный 30^{\circ}
. Поэтому треугольник COB
— равносторонний. Следовательно,
R=OC=BC=2.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 64, с. 40
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.1, с. 86
