283. Пусть O
— центр окружности, описанной около треугольника ABC
. Найдите угол OAC
, если: а) \angle B=50^{\circ}
; б) \angle B=126^{\circ}
.
Ответ. а) 40^{\circ}
; б) 36^{\circ}
.
Указание. Вписанный угол равен половине соответствующего центрального угла.
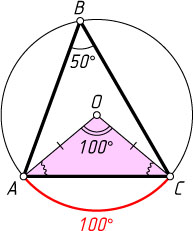
Решение. а) Угловая величина дуги AC
, не содержащей точки B
, равна 100^{\circ}
(рис. 1). Поэтому
\angle AOC=100^{\circ},~\angle OAC=40^{\circ}.
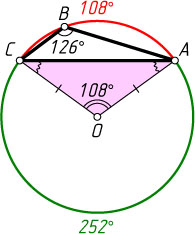
б) Угловая величина дуги ABC
равна 360^{\circ}-2\cdot126^{\circ}=108^{\circ}
(рис. 2). Поэтому
\angle AOC=108^{\circ},~\angle OAC=36^{\circ}.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 65, с. 40

