285. Два угла треугольника равны 50^{\circ}
и 100^{\circ}
. Под каким углом видна каждая сторона треугольника из центра вписанной окружности?
Ответ. 105^{\circ}
, 115^{\circ}
, 140^{\circ}
.
Указание. Центр окружности, вписанной в треугольник, есть точка пересечения биссектрис треугольника.
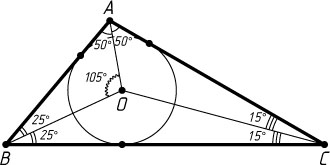
Решение. Если в треугольнике ABC
углы BAC
и ABC
равны 100^{\circ}
и 50^{\circ}
соответственно, то \angle ACB=30^{\circ}
. Поскольку центр O
вписанной окружности — точка пересечения биссектрис треугольника, то
\angle AOB=180^{\circ}-\frac{1}{2}\angle BAC-\frac{1}{2}\angle ABC=180^{\circ}-75^{\circ}=105^{\circ}.
Остальные углы находятся аналогично.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 67, с. 40
