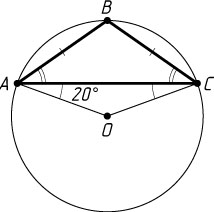
286. Треугольник ABC
— равнобедренный. Радиус OA
описанного круга образует с основанием AC
угол OAC
, равный 20^{\circ}
. Найдите угол BAC
.
Ответ. 35^{\circ}
или 55^{\circ}
.
Указание. Вписанный угол равен половине соответствующего центрального угла. Рассмотрите два случая расположения точек O
и B
относительно прямой AC
.
Решение. Если точки O
и B
лежат по разные стороны от прямой AC
, то
\cup ABC=\angle AOC=180^{\circ}-2\cdot20^{\circ}=140^{\circ}.
Тогда угол ABC
опирается на дугу, угловая величина которой равна
360^{\circ}-140^{\circ}=220^{\circ}.
Поэтому
\angle ABC=110^{\circ},~\angle BAC=\frac{180^{\circ}-110^{\circ}}{2}=35^{\circ}.
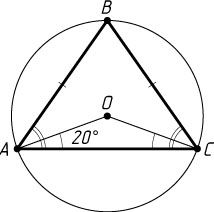
Если точки O
и B
лежат по одну сторону от прямой AC
, то аналогично находим, что \angle BAC=55^{\circ}
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 68, с. 40
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.3, с. 103

