292. С помощью циркуля и линейки впишите в данную окружность треугольник с двумя данными углами.
Указание. Вписанный угол вдвое меньше соответствующего центрального угла.
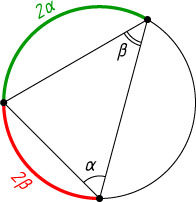
Решение. От произвольной точки данной окружности отложим две дуги вдвое большие данных углов так, чтобы выбранная точка была их единственной общей точкой. Выбранная точка и две полученные являются вершинами искомого треугольника.

Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 74, с. 41