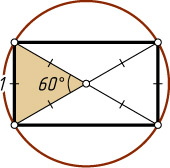
294. Меньшая сторона прямоугольника равна 1, острый угол между диагоналями равен 60^{\circ}
. Найдите радиус окружности, описанной около прямоугольника.
Ответ. 1.
Указание. Диагонали прямоугольника являются диаметрами описанной окружности.
Решение. Диагонали прямоугольника пересекаются в центре описанной окружности. Меньшая сторона прямоугольника видна из центра окружности под углом 60^{\circ}
. Следовательно, радиус окружности равен этой стороне, т. е. 1.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 76, с. 41
