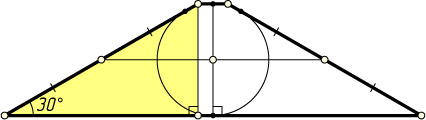
301. Около окружности описана равнобедренная трапеция с углом 30^{\circ}
. Её средняя линия равна 10. Найдите радиус окружности.
Ответ. 2,5.
Указание. Боковая сторона такой трапеции равна полусумме оснований.
Решение. Сумма оснований равна удвоенной средней линии, т. е. 20. Сумма боковых сторон равна сумме оснований. Поэтому боковая сторона трапеции равна 10, а высота трапеции равна половине боковой стороны, т. е. 5. Следовательно, радиус вписанной окружности равен 2,5.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 83, с. 41
