302. Во вписанном четырёхугольнике ABCD
диагональ AC
перпендикулярна диагонали BD
и делит её пополам. Найдите углы четырёхугольника, если \angle BAD=\alpha
.
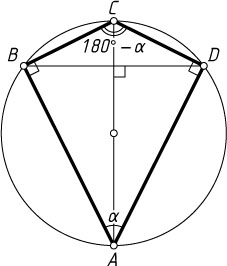
Ответ. 90^{\circ}
, 90^{\circ}
, 180^{\circ}-\alpha
.
Указание. Серединный перпендикуляр к хорде проходит через центр окружности.
Решение. Поскольку диагональ AC
— диаметр, то
\angle ABC=\angle ADC=90^{\circ}.
Поскольку \angle BAD
и \angle BCD
— противоположные углы вписанного четырёхугольника, то
\angle BCD=180^{\circ}-\angle BAD=180^{\circ}-\alpha.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 84, с. 41
