304. Центральный угол сектора равен 60^{\circ}
, а радиус равен R
. Найдите радиус окружности, вписанной в этот сектор.
Ответ. \frac{R}{3}
.
Указание. Линия центров двух касающихся окружностей проходит их через точку касания.
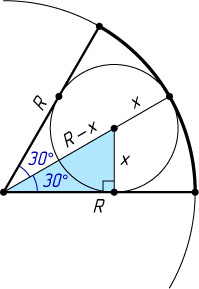
Решение. Обозначим искомый радиус через x
. Поскольку линия центров двух касающихся окружностей проходит через их точку касания, а катет, лежащий против угла в 30^{\circ}
равен половине гипотенузы, то R-x=2x
. Отсюда находим, что x=\frac{R}{3}
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 86, с. 41
