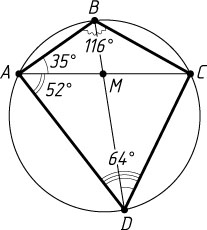
305. В выпуклом четырёхугольнике ABCD
дано: \angle ABC=116^{\circ}
, \angle ADC=64^{\circ}
, \angle CAB=35^{\circ}
и \angle CAD=52^{\circ}
. Найдите угол между диагоналями, опирающийся на сторону AB
.
Ответ. 81^{\circ}
.
Указание. Данный четырёхугольник — вписанный.
Решение. Пусть диагонали данного четырёхугольника пересекаются в точке M
. Поскольку
\angle ABC+\angle ADC=116^{\circ}+64^{\circ}=180^{\circ},
около данного четырёхугольника можно описать окружность. Искомый угол AMB
есть внешний угол треугольника AMD
. Поэтому он равен
\angle CAD+\angle ADB=52^{\circ}+\angle ADC-\angle BDC=
=52^{\circ}+64^{\circ}-35^{\circ}=81^{\circ}.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 87, с. 41
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.11, с. 103
