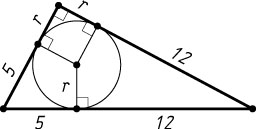
308. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки, равные 5 и 12. Найдите катеты треугольника.
Ответ. 8 и 15.
Указание. Выразите катеты через радиус вписанной окружности и воспользуйтесь теоремой Пифагора.
Решение. Обозначим радиус вписанной окружности через r
. Тогда катеты треугольника равны 5+r
и 12+r
. По теореме Пифагора
(5+r)^{2}+(12+r)^{2}=(5+12)^{2}.
Из этого уравнения находим, что r=3
.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.001, с. 158
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.12, с. 61
