309. Во вписанном четырёхугольнике ABCD
известно, что AB=a
, AD=b
(a\gt b
). Найдите BC
, если известно, что стороны BC
, CD
и AD
касаются некоторой окружности, центр которой находится на стороне AB
.
Ответ. a-b
.
Указание. Докажите, что AD+BC=AB
.
Решение. Пусть O
— центр окружности, о которой говорится в условии задачи. Тогда DO
и CO
— биссектрисы углов при вершинах D
и C
данного четырёхугольника.
Пусть \angle D=2\alpha
, \angle C=2\beta
, \alpha\gt\beta
. От луча DA
в полуплоскость, содержащую точку O
, отложим луч под углом \beta
. Поскольку \beta\lt\alpha
, этот луч проходит между сторонами угла ADO
, поэтому он пересекает сторону AB
в некоторой точке M
, лежащей между A
и O
,
\angle AMD=180^{\circ}-\angle ADM-\angle DAB=180^{\circ}-\angle ADM-(180^{\circ}-\angle BCD)=
=180^{\circ}-\beta-(180^{\circ}-2\beta)=\beta.
Поэтому треугольник ADM
— равнобедренный, AD=AM
, а \angle DMO=180^{\circ}-\beta
. Значит, точки D
, M
, O
и C
лежат на одной окружности.
Следовательно,
\angle CMB=\angle CMO=\angle CDO=\alpha,
\angle BCM=180^{\circ}-\angle CMB-\angle CBA=180^{\circ}-\alpha-(180^{\circ}-2\alpha)=\alpha.
Поэтому треугольник BMC
— также равнобедренный, BC=BM
. Следовательно,
AD+BC=AM+BM=AB,
откуда BC=AB-AD=a-b
.
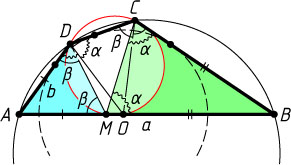
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 277, с. 31
