311. Сторона правильного треугольника равна a
. Найдите радиус вневписанной окружности.
Ответ. \frac{a\sqrt{3}}{2}
.
Указание. Докажите, что радиус искомой окружности равен высоте данного треугольника.
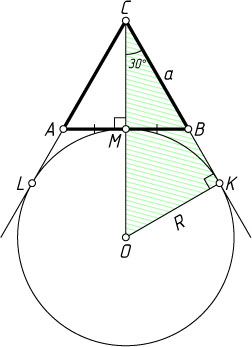
Решение. Пусть O
— центр окружности, касающейся стороны AB
равностороннего треугольника ABC
в точке M
(середина AB
) и продолжений сторон CA
и CB
в точках L
и K
соответственно. Если R
— искомый радиус, то
CO=2OK~(\angle OCK=30^{\circ}).
Поэтому CM+R=2R
. Следовательно,
R=CM=\frac{a\sqrt{3}}{2}.