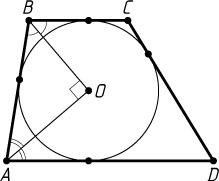
313. В трапецию вписана окружность. Докажите, что отрезки, соединяющие центр этой окружности с концами боковой стороны, перпендикулярны.
Указание. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
Решение. Пусть OA
и OB
— указанные отрезки. Тогда лучи AO
и BO
— биссектрисы углов при боковой стороне трапеции. Сумма этих углов равна 180^{\circ}
, сумма их половин равна 90^{\circ}
. Следовательно, угол AOB
— прямой.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.7, с. 30
