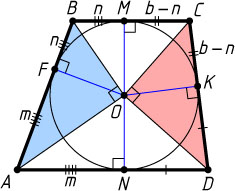
317. Окружность, вписанная в трапецию ABCD
, касается боковой стороны AB
в точке F
. Найдите площадь трапеции, если AF=m
, FB=n
, а меньшее основание трапеции BC
равно b
.
Ответ. \left(b+m+\frac{mn}{b-n}\right)\sqrt{mn}
.
Указание. Проведите радиус в точку касания со стороной AB
и примените теорему о высоте, опущенной из вершины прямого угла на гипотенузу.
Решение. Пусть O
— центр окружности; M
, K
, N
— точки касания со сторонами BC
, CD
, AD
соответственно, R
— радиус окружности. Тогда (см. задачу 656)
OF^{2}=BF\cdot AF=mn,~R=OF=\sqrt{mn},~CK=CM=CB-BM=b-n.
Поскольку OK^{2}=CK\cdot KD
, то
KD=\frac{mn}{b-n},~AD=AN+ND=m+\frac{mn}{b-n}.
Следовательно,
S_{ABCD}=\frac{BC+AD}{2}\cdot2R=\frac{1}{2}\left(b+m+\frac{mn}{b-n}\right)\cdot2\sqrt{mn}=\left(b+m+\frac{mn}{b-n}\right)\sqrt{mn}.
Источник: Вступительный экзамен в МФТИ. — 1971, билет 1, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 71-1-3, с. 145
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 168, с. 21
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 168, с. 20
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 7.23, с. 59
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — 10.410, с. 185
