320. В равнобедренную трапецию вписана окружность. Расстояние от центра окружности до точки пересечения диагоналей трапеции относится к радиусу как 3:5
. Найдите отношение периметра трапеции к длине вписанной окружности.
Ответ. \frac{5}{\pi}
.
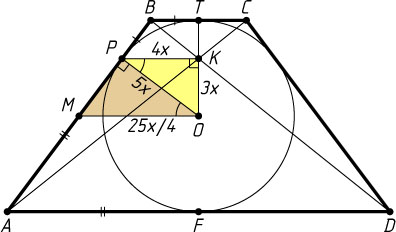
Указание. Отрезок, соединяющий точку пересечения диагоналей данной трапеции с точкой касания окружности и боковой стороны, параллелен основаниям трапеции.
Решение. Пусть O
— центр окружности, P
— точка касания с боковой стороной AB
, F
и T
— точки касания окружности с основаниями AD
и BC
, M
— середина AB
, K
— точка пересечения диагоналей AC
и BD
трапеции. Обозначим OK=3x
, OP=5x
.
Поскольку AP:PB=AF:BT=AK:KC
, то KP\parallel BC\parallel OM
. Из прямоугольного треугольника OKP
находим, что KP=4x
. Из подобия треугольников OKP
и MPO
находим, что
OM=\frac{OP^{2}}{KP}=\frac{25x}{4}.
Тогда периметр трапеции равен 8OM=50x
. Следовательно, искомое отношение равно
\frac{50x}{2\pi\cdot5x}=\frac{5}{\pi}.
Источник: Вступительный экзамен в МФТИ. — 1980, билет 2, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 80-2-3, с. 221
