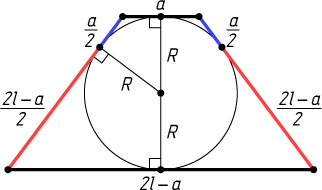
325. Около окружности описана равнобедренная трапеция с боковой стороной l
. Одно из оснований трапеции равно a
. Найдите площадь трапеции.
Ответ. l\sqrt{a(2l-a)}
.
Указание. Найдите второе основание и радиус вписанной окружности.
Решение. Сумма оснований данной трапеции равна сумме боковых сторон, т. е. 2l
; второе основание равно 2l-a
; отрезки, на которые точка касания вписанной окружности делит боковую сторону, равны \frac{a}{2}
и \frac{2l-a}{2}
; радиус вписанной окружности равен среднему геометрическому этих отрезков (см. задачу 656), т. е. \frac{1}{2}\sqrt{a(2l-a)}
; высота трапеции равна диаметру вписанного круга, т. е. \sqrt{a(2l-a)}
. Следовательно, площадь трапеции равна l\sqrt{a(2l-a)}
.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 37, с. 10
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 37, с. 8
