326. Площадь равнобедренной трапеции, описанной около окружности, равна S
. Найдите среднюю линию трапеции, если острый угол при её основании равен \alpha
.
Ответ. \sqrt{\frac{S}{\sin\alpha}}
.
Указание. Средняя линия данной трапеции равна боковой стороне.
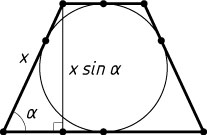
Решение. Пусть x
— средняя линия данной трапеции. Тогда боковая сторона также равна x
, а высота трапеции равна x\sin\alpha
. Имеем уравнение
S=x^{2}\sin\alpha.
Отсюда находим, что
x=\sqrt{\frac{S}{\sin\alpha}}.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1975, № 4, вариант 2
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.13, с. 30
