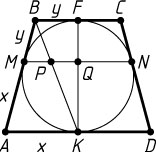
330. Около окружности описана равнобедренная трапеция ABCD
. Боковые стороны AB
и CD
касаются окружности в точках M
и N
, K
— середина AD
. В каком отношении прямая BK
делит отрезок MN
?
Ответ. 1:3
.
Указание. Докажите, что MN
параллельно основаниям трапеции и рассмотрите подобные треугольники.
Решение. Обозначим x=AK
, y=BF
, где F
— середина BC
. Пусть Q
— точка пересечения KF
и MN
, а P
— точка пересечения MN
и BK
. Тогда
AM=AK=x,~BM=BF=y
и Q
— середина MN
.
Поскольку MN
параллельно основаниям трапеции, то треугольник BMP
подобен треугольнику BAK
, а треугольник KPQ
подобен треугольнику KBF
. Поэтому
\frac{PM}{x}=\frac{y}{x+y},~\frac{PQ}{y}=\frac{x}{x+y}.
Следовательно, PM=PQ
и PM=\frac{1}{4}MN
.
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 218, с. 208
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 688, с. 87
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 6.17, с. 47
