335. Около окружности радиуса R
описана трапеция. Хорда, соединяющая точки касания окружности с боковыми сторонами трапеции, равна a
. Хорда параллельна основанию трапеции. Найдите площадь трапеции.
Ответ. \frac{8R^{3}}{a}
.
Указание. Докажите, что данная трапеция равнобедренная. Проведите радиус в точку касания вписанной окружности с боковой стороной трапеции, соедините центр окружности с серединой боковой стороны и рассмотрите получившиеся подобные треугольники.
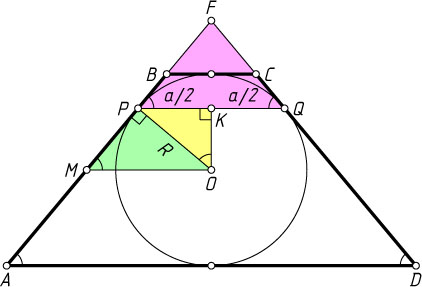
Решение. Пусть O
— центр окружности, P
и Q
— точки касания окружности с боковыми сторонами AB
и CD
трапеции ABCD
, K
и M
— середины PQ
и AB
соответственно.
Продолжив AB
и CD
до пересечения в точке F
, получим равнобедренный треугольник QFP
. Следовательно, трапеция ABCD
— равнобедренная. Половину средней линии, отрезок MO
, найдём из подобия треугольников PKO
и OPM
.
Источник: Вступительный экзамен на биологический факультет МГУ. — 1979, вариант 1, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 52
