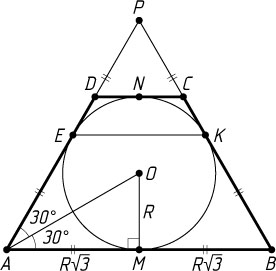
336. Около окружности радиуса R
описана равнобедренная трапеция ABCD
; E
и K
— точки касания этой окружности с боковыми сторонами AD
и BC
. Угол между основанием AB
и боковой стороной AD
трапеции равен 60^{\circ}
. Докажите, что EK
параллельно AB
и найдите площадь трапеции ABKE
.
Ответ. \frac{9R^{2}\sqrt{3}}{4}
.
Указание. Для доказательства параллельности EK
и AB
продолжите боковые стороны до их пересечения. Для нахождения элементов трапеции ABKE
рассмотрите равносторонний треугольник AEM
(M
— середина AB
).
Решение. Пусть M
и N
— точки касания окружности с основаниями AB
и CD
соответственно, а точки E
и K
лежат на боковых сторонах соответственно AD
и BC
трапеции ABCD
. Поскольку трапеция равнобедренная, точки M
и N
— середины оснований. Отрезки касательных, проведённых к окружности из одной точки, равны, поэтому
DE=DN=NC=CK,~AE=AM=MB=BK,
Значит, \frac{DE}{AE}=\frac{CK}{BK}
, причём AB\parallel CD
. Следовательно, EK\parallel AB
.
Продолжим боковые стороны трапеции до пересечения в точке P
. Тогда треугольник ABP
равносторонний, а окружность радиуса R
, вписанная в трапецию ABCD
, — вписанная окружность треугольника ABC
. Значит, точки E
и K
— середины сторон AP
и BP
этого треугольника. Тогда EK
— его средняя линия, поэтому S_{\triangle PEK}=\frac{1}{4}S_{\triangle ABP}
.
Пусть O
— центр окружности. Тогда AO
— биссектриса угла BAP
, равного 60^{\circ}
. Из прямоугольного треугольника AOM
находим, что AM=OM\ctg\angle OAM=R\ctg30^{\circ}=R\sqrt{3}
, поэтому
AP=BP=AB=2R\sqrt{3},~S_{\triangle APB}=\frac{AB^{2}\sqrt{3}}{4}=\frac{12R^{2}\sqrt{3}}{4}=3R^{2}\sqrt{3}.
Следовательно,
S_{ABKE}=\frac{3}{4}S_{\triangle APB}=\frac{3}{4}\cdot3R^{2}\sqrt{3}=\frac{9R^{2}\sqrt{3}}{4}.
Источник: Вступительный экзамен на химический факультет МГУ. — 1971, № 1, вариант 1
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 8.34, с. 76
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 8.34.1, с. 83
