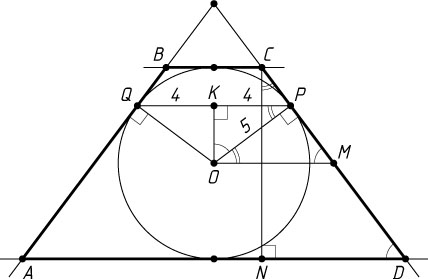
337. В некоторый угол вписана окружность радиуса 5. Хорда, соединяющая точки касания, равна 8. К окружности проведены две касательные, параллельные хорде. Найдите стороны полученной трапеции.
Ответ. 5, 20, \frac{25}{2}
, \frac{25}{2}
.
Указание. Треугольник PKO
с вершинами в точке касания окружности с боковой стороной, в середине данной хорды и в центре окружности, подобен треугольнику OPM
, где M
— середина боковой стороны полученной трапеции.
Решение. Пусть O
— центр окружности, P
и Q
— точки касания окружности с боковыми сторонами CD
и AB
полученной равнобедренной трапеции ABCD
, K
— середина PQ
, M
— середина CD
.
Из подобия треугольников PKO
и OPM
следует, что
\frac{OP}{OM}=\frac{KP}{OP},~OM=\frac{OP^{2}}{KP}=\frac{25}{4}.
Поскольку средняя линия трапеции равна \frac{25}{2}
, то
CD=AB=\frac{25}{2}.
Пусть N
— проекция вершины C
на большее основание AD
. Из подобия треугольников CND
и PKO
находим, что
\frac{ND}{KO}=\frac{CN}{KP},~ND=\frac{CN\cdot KO}{KP}=\frac{10\cdot3}{4}=\frac{15}{2},
а так как отрезок AN
равен средней линии трапеции, то AN=\frac{25}{2}
. Следовательно,
AD=AN+ND=\frac{25}{2}+\frac{15}{2}=20,~BC=AD-2ND=20-15=5.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.205, с. 172
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.17, с. 112
