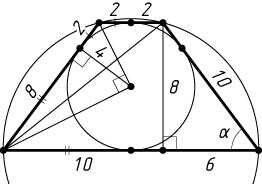
338. Основания трапеции равны 4 и 16. Найдите радиусы окружностей, вписанной в трапецию и описанной около неё, если известно, что эти окружности существуют.
Ответ. 4; \frac{5\sqrt{41}}{4}
.
Указание. Радиус вписанной окружности равен среднему геометрическому отрезков, на которые точка касания делит боковую сторону.
Решение. Поскольку трапеция вписанная, то она — равнобедренная. Пусть r
и R
— радиусы вписанной и описанной окружностей.
Точка касания вписанной окружности делит боковую сторону на отрезки 2 и 8. Поэтому r=\sqrt{2\cdot8}=4
(см. задачу 656).
Диагональ трапеции — гипотенуза прямоугольного треугольника с катетами 8 (высота трапеции, опущенная из вершины меньшего основания на большее) и 10 (проекция диагонали на большее основание, равная длине средней линии). Эта диагональ видна из вершины большего основания трапеции под углом \alpha
, синус которого равен \frac{4}{5}
(угол боковой стороны с основанием). Следовательно,
R=\frac{\sqrt{8^{2}+10^{2}}}{2\sin\alpha}=\frac{2\sqrt{41}}{\frac{8}{5}}=\frac{5\sqrt{41}}{4}.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.199, с. 172
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.17, с. 31
