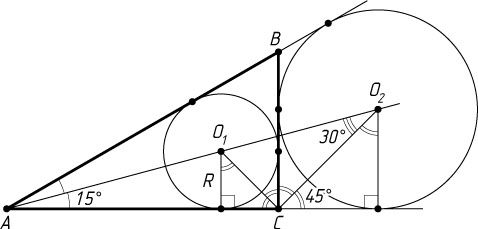
340. В прямоугольный треугольник ABC
с углом A
, равным 30^{\circ}
, вписана окружность радиуса R
. Вторая окружность, лежащая вне треугольника, касается стороны BC
и продолжений двух других сторон. Найдите расстояние между центрами этих окружностей.
Ответ. 2R\sqrt{2}
.
Указание. Пусть O_{1}
и O_{2}
— центры данных окружностей, C
— вершина прямого угла треугольника ABC
. Тогда треугольник O_{1}CO_{2}
— прямоугольный. Найдите его углы.
Решение. Пусть O_{1}
и O_{2}
— центры данных окружностей (R
— радиус первой), C
— вершина прямого угла. Тогда треугольник O_{1}CO_{2}
— прямоугольный. Поскольку точки O_{1}
и O_{2}
расположены на биссектрисе угла A
, то
\angle O_{1}O_{2}C=75^{\circ}-45^{\circ}=30^{\circ}.
Следовательно,
O_{1}O_{2}=2O_{1}C=2R\sqrt{2}.
Источник: Вступительный экзамен на химический факультет МГУ. — 1971, № 1, вариант 2
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.13, с. 87
