343. Средняя линия равнобедренной трапеции равна 5. Известно, что в трапецию можно вписать окружность. Средняя линия трапеции делит её на две части, отношение площадей которых равно \frac{7}{13}
. Найдите высоту трапеции.
Ответ. 4.
Указание. Решите систему уравнений с двумя неизвестными — длинами оснований трапеции.
Решение. Пусть x
и y
— основания трапеции. Тогда
\syst{x+y=10\\\frac{x+5}{y+5}=\frac{7}{13}.\\}
Отсюда находим, что x=2
и y=8
. Следовательно, боковая сторона трапеции равна 5.
Опустим высоту из вершины верхнего основания на нижнее и найдём её по теореме Пифагора.
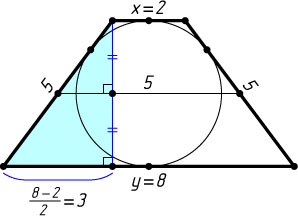
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1977, № 2, вариант 2
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 6
