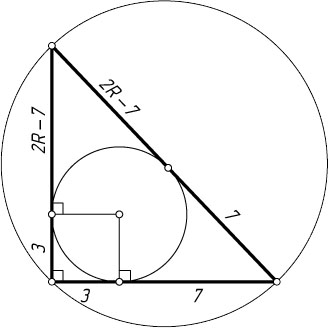
345. Найдите радиус окружности, описанной около прямоугольного треугольника, если радиус окружности, вписанной в него, равен 3, а катет равен 10.
Ответ. \frac{29}{4}
.
Указание. Гипотенуза — диаметр описанной окружности.
Решение. Пусть R
— искомый радиус. Тогда гипотенуза равна 2R
. Поскольку радиус вписанной окружности равен 3, то катет, равный 10, делится точкой касания на отрезки, равные 7 и 3. Тогда второй катет равен
3+2R-7=2R-4.
Применим теорему Пифагора к данному треугольнику и найдём R
из полученного уравнения.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.050, с. 162
