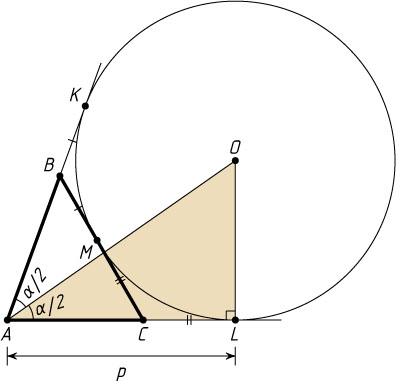
349. В треугольнике ABC
с периметром 2p
острый угол BAC
равен \alpha
. Окружность с центром в точке O
касается стороны BC
и продолжений сторон AB
и AC
в точках K
и L
соответственно. Найдите площадь треугольника AOL
.
Ответ. \frac{1}{2}p^{2}\tg\frac{\alpha}{2}
.
Указание. Отрезки касательных, проведённых из одной точки к окружности, равны между собой.
Решение. Пусть M
— точка касания данной окружности со стороной BC
. Тогда
KB=BM,~LC=CM,~2p=AB+BC+AC=AK+AL,
а так как AK=AL
, то AL=p
. Поэтому
OL=AL\tg\frac{\alpha}{2}=p\tg\frac{\alpha}{2}.
Следовательно,
S_{\triangle AOL}=\frac{1}{2}AL\cdot LO=\frac{1}{2}p^{2}\tg\frac{\alpha}{2}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1983, № 3, вариант 2
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — № 3, с. 14
